都立中高一貫校の適性検査と私立中学校の教科型試験は、問題や解答方法の傾向に違いがあります。
全体的な特徴については以前説明した通りです。
こちらをどうぞ→「適性検査(都立中学受検)と教科型試験(私立中学受験)の勉強法はなぜ違うのか?」
ここからは、さらに詳しく教科別に説明したいと思います。
今回は算数です。
この記事では算数分野での適性検査と教科型試験の違いを説明します。
実際の問題を見ると違いがはっきりわかるので、試しに、植木算の考え方を使った問題をとりあげてみましょう。(適性検査の問題は植木算と言えないかもしれませんが…)
参考までに)植木算とは?
30mの道の端から端に3mおきに木を植えていくと何本植えることになるか、というような問題です。
30m÷3m=10で間隔の数は10個ですが…
両端に植えるとすると、間隔の数より木の本数は1本増え、11本となります。
逆に両端に植えないと間隔の数より 木の本数は 1本減り、9本となります。
また、池のような円形のところで行うと間隔の数と木の本数は等しくなります。
短文からポイントを読み取る教科型試験
まずは、教科型試験の例題からみていきましょう。
半径99mの円形の池の周りに池から1mはなして、黄色、白、赤の3色の花を2mおきに植えます。地点Aから黄色、赤、白の順に植えるとき、花の数は黄色は 1⃣ 、白は 2⃣ 、赤は 3⃣ です。円周率は3.14とします。
私立入試問題・例題(湘南白百合学園中学校入試問題より)
この問題では、池=円状=端はないこと、半径99mの池から1mをはなす=100mの半径の円の円周上に植えること、3色が同じ本数植えられないかもしれないこと(余りが出た時の処理を正しくすること)、円周を正しい計算で求められるか、などがポイントです。
私立中学受験の勉強では同じような問題を演習問題として何度も解いているので、花を池に植えると読んだ時点で、間隔の数と本数の問題に注意するあれだな、ピンとくるわけです。
そして、円周では細かい条件を気を付けて…と図をかいたりして慎重に解くのがセオリーでしょう。
このように、教科型試験の問題では、さらっと書かれた短い問題文の中に多くの重要となる言葉が隠されています。
問題文を読むのに時間はかかりませんが、読みながら重要なポイントをしっかりおさえなければなりません。そして、できるだけ速く正確に計算することが大切です。
教科型試験では、短文から、いかに正確な状況を把握できるかが最重要ポイントです。
長文から条件を拾い出す適性検査
次に、適性検査の例題をみてみましょう。
適性検査・例題(2020年度共同問題より)
先生、花子さん、太郎さんが、校内の6年生と4年生との交流会に向けて話をしています。
先生:今度、学校で4年生との交流会が開かれます。6年制59人は、制作した作品を展示して見てもらいます。また、4年生といっしょにゲームをします。
花子:楽しそうですね。私たち6年生は、この交流会に向けて一人1枚画用紙に動物の絵をかいたので、それを見てもらうのですね。絵を展示する計画を立てましょう。
先生:みんなが絵をかいたときに使った画用紙の辺の長さは、短い方が40㎝、長い方が50㎝です。画用紙を横向きに使って絵をかいたものを横向きの画用紙、画用紙を縦向きに使って絵をかいたものを縦向きの画用紙と呼ぶことにします。
太郎:図1の横向きの画用紙と、図2の縦向きの画用紙は、それぞれ何枚ずつあるか数えてみよう。
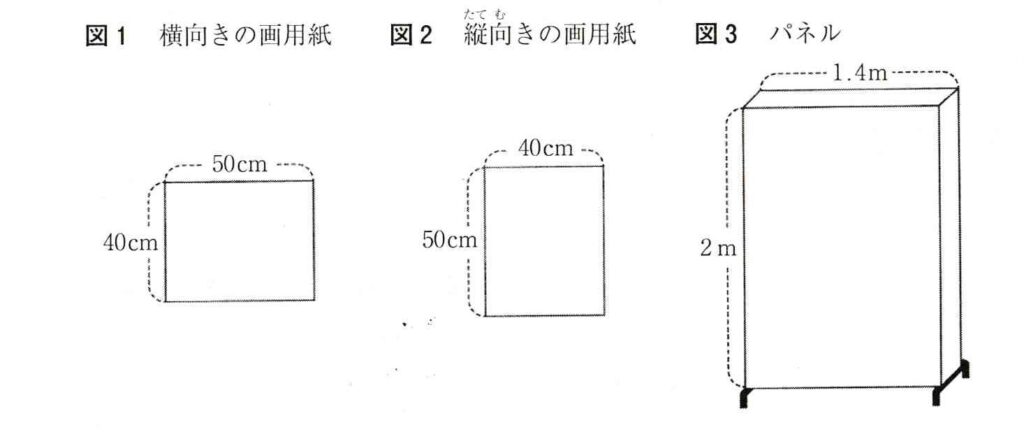
花子:横向きの画用紙は38枚あります。縦向きの画用紙は21枚です。全部で59枚ですね。
太郎:先生、画用紙はどこにはればよいですか。
先生:学校に、図3のような縦2m、横1.4mのパネルがあるので、そこにはります。絵はパネルの両面にはることができます。
花子:分かりました。ところで、画用紙をはるときの約束はどうしますか。
先生:作品が見やすいように、画用紙をはることができるとよいですね。昨年は、次の[約束]したがってはりました。
[約束]
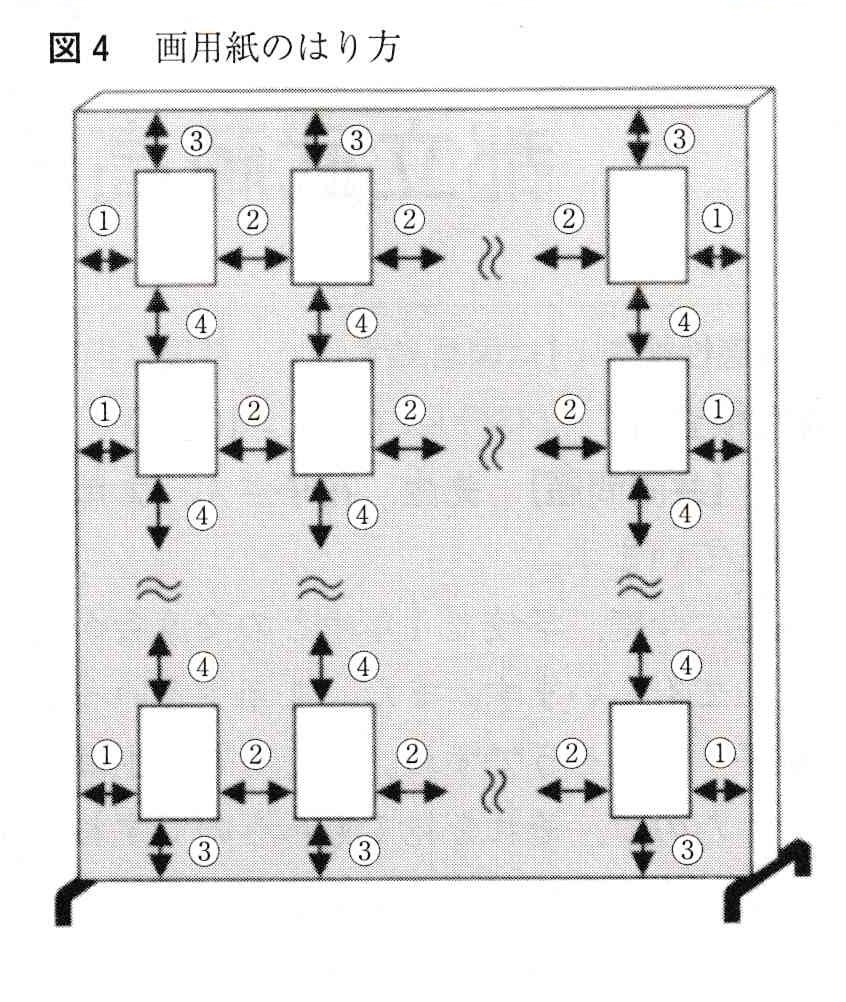
(1)図4のように、画用紙はパネルの外にはみ出さないように、まっすぐにはる。
(2) パネルの一つの面について、どの行(横のならび)にも同じ枚数の画用紙をはる。また、どの列(縦のならび)にも同じ枚数の画用紙をはる。
(3)1台のパネルに、はる面は2面ある。一つの面には、横向きの画用紙と縦向きの画用紙を混ぜてはらないようにする。
(4) パネルの左右のはしと画用紙の間の長さを①、左の画用紙と右の画用紙の間の長さを②、パネルの上下のはしと
画用紙の間の長さを③、上の画用紙と下の画用紙の間の長さを④とする。
(5) 長さ①どうし、長さ②どうし 、長さ③どうし 、長さ④どうし はそれぞれ同じ長さとする。
(6) 長さ①~④はどれも5㎝以上で、5の倍数の長さ(㎝)とする。
(7) 長さ①~④は、面によって変えてもよい。
(8) 一つの面にはる画用紙の枚数は、面によって変えてもよい。
花子:今年も昨年の [約束]と同じように、パネルをはることにしましょう。
太郎:そうだね。例えば、図2の縦向きの画用紙6枚を、パネルの一つの面にはってみよう。いろいろなはり方がありそうですね。
問題1 [約束] にしたがって、図3のパネルの一つの面に、図2で示した縦向きの画用紙6枚をはるとき、あなたなら、はるときお長さ①~④をそれぞれ何cmにしますか。
花子:次に、6年生の作品の、横向きの画用紙38枚と、縦向きの画用紙21枚のはり方を考えていきましょう。
太郎:横向きの画用紙をパネルにはるときも、 [約束] にしたがってはればよいですね。
花子:先生、パネルは何台ありますか。
先生:全部で8台あります。しかし、交流会と同じ時期に5年生もパネルを使うので、交流会で使うパネルの台数はなるべく少ないほうがよいですね。
太郎:パネルの台数を最も少なくするために、パネルの面にどのように画用紙をはればよいか考えましょう。
問題2 [約束] にしたがって、6年生の作品59枚をはるとき、パネルの台数が最も少なくなるときのはり方について考えます。そのときのパネルの台数を答えなさい。また、その理由を、それぞれのパネルの面に、どの向きの画用紙を何枚ずつはるか具体的に示し、文章で説明しなさい。なお、長さ①~④については説明しなくてよい。
以上です。読むのにどれ位かかったでしょうか?
問題数が倍の2問とはいえ、文の長さに驚きませんか?
「楽しそうですね」などの問題には関係のない話し言葉も含まれ、無駄に長いですね。「交流会」の件も問題を解く上ではまったく不要な情報です。
適性検査の問題では、必ずこのような会話文によって問題が構成されています。
さて、問題1では、 横40cm, 縦60cmの画用紙6枚を 縦2m、横1.4mのパネルのオモテ面に貼ることだけを考えれば良いのですが、画用紙と画用紙の間隔がいくつあるかを考えるときに植木算的考え方を使います。
けれども、実際には2枚か3枚しか並べられないので、図にかいてしまえば一目瞭然です。
ここで重要なことは膨大な情報量から、間隔を5の倍数とすることや、どの行、どの列にも同じ枚数の画用紙を貼ることを読み落とさないことです。
また、もう一つ、適性検査の特徴と言えるのは、答えは何パターンもある、ということです。
これは私立受験用の勉強をしてきたお子さんにとってはおそらく戸惑うポイントの1つです。
答えが1つに決まらないという点は、当てはまるものを全て答えることに慣れていると不安になるものです。
以上よりまとめると、適性検査の算数分野で大切なのは、長文の中から重要な条件を漏らさずに探し出すことです。
解き方はそれほど変わらない
上で述べたように出題形式は大きく異なりますが、答えを考える過程で使う考え方は、算数分野では教科型試験も適性検査もそれほど違いはない、と私は思います。
問題を読みとるのに時間や力が必要ない分、若干教科型試験の方が難易度は高めな印象ですが、適性検査でも数列や速度の計算法、図形の基本計算などの基礎力が重要であるのは同じです。
適性検査ではひっかけのような問題や複雑すぎる問題はあまり出されない傾向があるので、学校で習うような基本的な知識や数学公式が身についていれば解くことができます。
例えば、半径3cmの半円の面積、50㎞/時の車が10㎞先にいる40㎞/時の車に追いつくのは何分後か、12と18の最大公約数、底辺が5㎤で高さ6cmの三角錐の体積…このような基本的な問題が全ての単元において、抵抗なく時間をかけずにできれば問題はありません。
ただ、私が想像するに、おそらく宿題などをしっかりとこなしていて習ったときは理解できていても違う単元を学んでいるうちに忘れてしまうものではないでしょうか。
また、適性検査では、読みとるのに時間をとられるために計算や基本的な公式を思い出すための時間ロスは致命的です。
このような問題を解決するために、算数に関しては教科型試験の勉強をしておくことを私はおすすめしたいです。
反復練習できるだけでなく、難易度の高い問題に取り組むことで思考力も身につきます。
適性検査の過去問を行うだけでは、全ての範囲を網羅できていない気がして不安な気持ちになりますが、その不安も一掃できます。
教科型試験の勉強をしておくとよい理由をまとめると以下の通りです。
- 全範囲が網羅できる。
- 適性検査対策のみをしている受検生よりも算数力が付くため有利。
- 過去問に取り組む段階で基礎的な内容でつまずくことがなく、たくさんの問題に取り組める。
- 円周率を使った計算など、面倒な計算にも抵抗がなくなる。
- 入学後の授業にも難なく付いていける。
おすすめは小学4年生からの進研ゼミ中学受験講座
教科型試験の勉強をするためにはどうすればよいかと考えた時、最も一般的な選択は塾に通うことだと思います。
塾に通うとどうなるか…おそらく私立受験を行う流れになります。
教科型試験は主に私立試験で採用されていて、勉強する量も多いので、教科型試験を勉強しながら都立中高一貫だけ受検する子はほとんどいません。塾の先生、周りのお子さん、保護者の方から影響を受けて私立受験する方針に変わると思います。
私は私立受験をすることは考えていず、経済的にも、子どもの生活時間にも、あまり負荷をかけたくなかったので、塾に通いたくはありませんでした。
では塾に行かずに、問題集を買って自分でカリキュラムを組むのか、と考えた時、私の知識や能力ではとても無理だと判断し、通信講座を利用しました。
結果的に内容に満足し、とてもおすすめです。
塾と比べたらかなり格安で、しっかり取り組むことができれば通塾と変わらない学力がつきます。
カリキュラムも丁寧に設定されていて、毎月モデルスケジュールが組まれたカレンダーも付いてくるので、取り組みやすいです。
算数に関しては難しいと感じる子も多いため、4年生から始めるのがおすすめです。
4年生から始めれば、内容が簡単で量も少ないので、取り組みやすいです。
また、4年生から学習習慣を付けておけば、学校での学習が難易度を増してくる5年次に慌てることなく落ち着いて進級できます。
5年、6年の成績も上がるので報告書対策もばっちりです。
ご興味がある方は、以下のリンク内の「中学受験対策」から資料請求、講座申し込みが可能です。
【進研ゼミ小学講座】適性検査対策はとにかく過去問。過去問題集は「思考力で合格!」がおすすめ
教科型試験の勉強だけでは、問題形式や解答方法に慣れることができないので、小学6年からは適性検査の過去問を解きましょう。
我が家では過去問は、Z会公立中高一貫校適性検査5年生/6年生、公立中高一貫校適性検査問題集全国版(銀本)、過去問をまとめた問題集、志望校の過去問に取り組みました。
当初はこんなに真剣に受検対策をするつもりはなく(無理なく勉強を続けて受けるだけ受けてみるつもりでした)Z会の講座だけでもいいかなぁと思っていたのですが、直前(小6の11月)で息子がやる気になり、もっと問題を解きたいと言うのでどんどん増えました。
正直、6年生で過去問の問題集を買ってどんどん取り組むつもりなら、重なる部分も多いので6年生のZ会の講座は受けなくても良かったような気がします。
5年生の時に、適性検査ってどんな感じかなぁと知りたい場合は、進研ゼミと両立できる量としてZ会の講座はちょうどいいと思います。
時期としては進研ゼミを受けているなら6年生からで十分だと個人的には思います。我が家は小学6年生の9月ごろから、過去問に取り組みましたが、もう少し余裕を持って取り組めた方が良かったと思います。
過去問をまとめた問題集の中では「思考力で合格!」がおすすめです。
算数分野だけまとまっていて、都立の出題傾向に合っています。難しめの問題も多いので、解きごたえがあります。解説が丁寧なので、丸付けもしやすく、どのような問題があり、どのように答えるか、と知るのに適しています。
ただ1つ、問題と解答が分かれていず、解答が問題の続きに書かれているために、あらかじめ隠して解かないと解答が見えてしまうのがとても不便です。(マステで紙を貼って隠してました)
おすすめの順番としては、
Z会公立中高一貫校適性検査5年生(5年生から少しやってみたいなら)
→思考力で合格!→志望校の過去問(近年の分を残す)→銀本→志望校の過去問(近年の分)
です。
気を付けたいのは、問題集は過去問を集めた物なので、志望校の過去問も含まれていることです。
志望校の過去問を後で時間を計って通して取り組みたい場合は、志望校の問題は飛ばして解きましょう。
(都立の共同問題も飛ばしましょう。)
Z会の公式ホームページのリンクを張っておきます。具体的な内容についてはこちらのリンク先の情報を確認してみてください。
資料請求用のリンクも張っておきます。ご興味ある方は下記リンクから申し込みしてください。
※資料請求するだけでもらえる「おためし教材」もあります。
こちらは銀本へのリンクです。
まとめ
- 算数分野では、教科型試験と適性検査は出題形式が大きく異なるが、根本的な解き方はそれほど変わらない。
- 教科型試験の勉強をしておけば、適性検査で必要な基礎知識、計算力、思考力を鍛えられる。
- 都立中高一貫校を志望するならば、塾に通わず小学4年生から通信講座(進研ゼミ中学受験講座)を受けるのがおすすめ。
- 適性検査対策は過去問をひたすら解くのがおすすめ。時期は6年生からでも遅くはない。
以上、算数分野について教科型試験と適性検査の違いや対策についてまとめてみました。
最後までお読みいただきありがとうございました。少しでもご参考になれば嬉しいです。
もしよろしければ他の教科の記事もご覧ください。









コメント